Monte Carlo
De formule van Leibniz uit de vorige oefening gaf ons een schatting van \(\pi\), maar je hebt misschien gemerkt dat deze schatting niet zo goed is: we hebben heel hoge waarden van \(n\) nodig vooraleer \(\pi_n\) dichtbij \(\pi\) komt. In deze oefening gaan we kijken naar een andere manier om \(\pi\) te schatten: Monte Carlo simulatie. Het inzicht achter dit algoritme wordt geïllustreerd in volgende afbeelding:
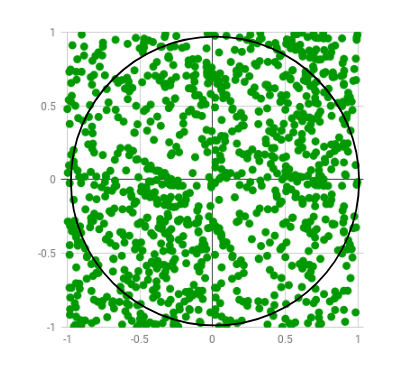
Wiskundig gezien is de oppervlakte van het gebied binnen de eenheidscirkel gedeeld door de totale oppervlakte van de ruimte exact gelijk aan \(4\pi\). We kunnen deze verhouding benaderen door willekeurig punten te kiezen in het vlak (de groene punten in de illustratie) en te tellen hoeveel daarvan er binnen en buiten de cirkel liggen. Concreet gaan we als volgt te werk:
- Genereer een willekeurig punt in het vlak. Dit is een koppel \((x,y)\) waar zowel \(x\) als \(y\) uniform in het interval \([0,1]\) gekozen worden.
- Controleer of dit punt binnen de eenheidscirkel ligt. Hiervoor moet je nagaan of \( x^2 + y^2 \leq 1 \).
- Als het punt in de cirkel ligt, tel dit dan bij het aantal punten in de cirkel op.
- Tel het totaal aantal punten op.
Herhaal dit algoritme een vast aantal keren. Als \(n\) het totaal aantal punten in de cirkel voorstelt en \(m\) het totaal aantal punten in het algemeen, dan is onze benadering voor \(\pi\) gegeven door
$$ \pi \approx 4\frac{n}{m}. $$
Voor deze oefening zijn de punten in het vlak al gegeven; jij moet ze enkel nog nakijken om te zien welke fractie in de eenheidscirkel ligt, zodat je een benadering van \(\pi\) kunt teruggeven.
Opgave
Schrijf een programma dat een lijst van punten in het vlak inleest en een Monte Carlo benadering berekent van \(\pi\) op basis van deze punten. Elke regel van het bestand bestaat uit twee kommagetallen gescheiden door een enkele spatie. Bijvoorbeeld:
-0.9137017706898813 -0.7368506597969771
Lees al deze punten in en bepaal welke fractie ervan in de eenheidscirkel ligt. Gebruik dit om een benadering van \(\pi\) te bepalen zoals hierboven beschreven.