Priemfactorisatie
Een priemgetal is een natuurlijk getal verschillend van 1 dat enkel maar deelbaar is door 1 en zichzelf. Zo zijn 2, 5 en 101 bijvoorbeeld priemgetallen, maar 1, 6 en 100 bijvoorbeeld niet. Het is een wiskundig feit dat elk natuurlijk getal \(n \in \mathbb{N}\) geschreven kan worden als een product van machten van priemgetallen:
$$ n = p_1^{a_1} \dots p_k^{a_k}. $$
Dit noemen we een priemfactorisatie of ontbinding in priemfactoren. Het getal 2020 kan bijvoorbeeld ontbonden worden in de volgende priemfactoren:
$$ 2020 = 2^2 \times 5 \times 101. $$
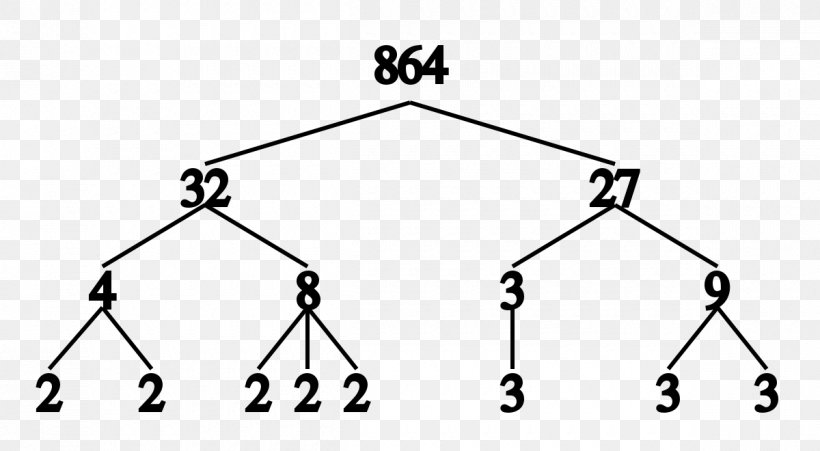
Het simpelste algoritme om priemfactorisaties te bepalen, is trial division. Hierbij ga je voor een getal \(n\) als volgt te werk:
- Voor elk getal \(k\) tussen 1 en \(n\) (\(1 < k < n\)), controleer of \(n\) deelbaar is door \(k\).
- Indien ja, dan is \(k\) een priemfactor van \(n\). Voeg \(k\) toe aan de verzameling priemfactoren en herhaal het algoritme voor \(n/k\).
- Indien nee, incrementeer \(k\). Stop het algoritme indien \(k \geq n\). In dat geval was \(n\) al een priemgetal.
We kunnen dit bijvoorbeeld toepassen op 2020:
- Start met \(k = 2\). Het getal 2020 is deelbaar door 2, dus we rekenen 2 als priemfactor en gaan verder met \(2020/2 = 1010\).
- Het getal \(1010\) is deelbaar door \(k = 2\), dus we rekenen 2 opnieuw als priemfactor en gaan verder met 505.
- We hebben geen succes met \(k = 3\) of \(k = 4\), maar wel met \(k = 5\). We voegen 5 toe als priemfactor en gaan verder met \(505/5 = 101\).
- We hebben geen succes voor \(k = 5, \dots, 100\). We besluiten dat 101 een priemgetal is en voegen het toe aan de factorisatie.
We hebben dus twee keer 2 geteld, één keer 5 en één keer 101.
Opgave
Schrijf een Python-programma dat een lijst van getallen neemt als invoer en hun priemfactorisatie uitschrijft als uitvoer. De invoer aan het programma is een lijst van getallen die gefactoriseerd moeten worden. Als uitvoer moet het programma voor elk getal een lijst van koppels teruggeven die de priemfactorisatie beschrijven. Zo moet het getal 2020 bijvoorbeeld volgende lijst opleveren als uitvoer:
[(2, 2), (5, 1), (101, 1)]
Dit is een lijst van koppels \( [(p_1, a_1), (p_2, a_2), (p_3, a_3)] \) waar \(p_1, p_2, p_3\) de priemgetallen zijn uit de factorisatie van 2020 (hier dus 2, 5 en 101) en \(a_1, a_2, a_3\) zijn de overeenkomstige exponenten (2, 1 en 1). Zorg ervoor dat deze lijst gesorteerd is zodat de priemgetallen in stijgende volgorde staan.
Voorbeeld
Invoer:
2020
1994
1998
1830
Uitvoer:
[(2, 2), (5, 1), (101, 1)]
[(2, 1), (997, 1)]
[(2, 1), (3, 3), (37, 1)]
[(2, 1), (3, 1), (5, 1), (61, 1)]